[M] 75. 顏色分類 (Sort Colors)
題目
- LeetCode 連結
- 主題:Array
- 難度:Medium
題目描述
給定一個包含 n 個物件的陣列 nums,每個物件被染成紅色、白色或藍色。請你就地 (in-place) 排序這些物件,使得相同顏色的物件相鄰,並按照紅色、白色、藍色的順序排列。
我們用整數 0、1 和 2 分別表示紅色、白色和藍色。你必須在不使用內建排序函式的情況下解決這個問題。
就地 (in-place) 意思為盡可能不利用其他大量空間來達成,通常傾向使用原始資料結構直接操作。
範例 1
輸入:nums = [2,0,2,1,1,0]
輸出:[0,0,1,1,2,2]範例 2
輸入:nums = [2,0,1]
輸出:[0,1,2]限制條件
n == nums.length1 <= n <= 300nums[i]為0、1或2之一
進階挑戰
你是否能設計一個只需遍歷一次且只使用常數額外空間的演算法?
問題釐清
- 輸入至少會有一個數字,且一定為
0,1,2,不需處理非法輸入? - in-place 的意思是,不需要有輸出,而是期待直接去改掉輸入陣列中的排序?
- 這題的範例看起來期待結果是升序排序?
- 基本實作能夠先不受遍歷一次的限制?
提出測試案例
- 能通過題目兩個範例
- 只有一個數字的輸入
- 全部同色的測試
- 完全反序的 300 個數字狀況
提出思路
因為題目要求一定需要 in-place,但輸入只有三種值,想到一個相對直覺的方式是可以做個 count map 去先用迴圈算出三種顏色分別出現幾次後,將原本輸入陣列去跑迴圈依數量取代當前數字,算是跑兩次迴圈的方式。用註解表示:
function sortColors(nums: number[]): void {
// declare count map
// run a for loop to count each amount of color
// run a for loop to replace input nums with count map
}實作
因為輸入只有三種數字,稍微改一下型別:
function sortColors(nums: (0 | 1 | 2)[]): void {
// declare count map
const counts = [0, 0, 0];
// run a for loop to count each amount of color
for (let num of nums) {
counts[num]++;
}
// run a for loop to replace input nums with count map
for (let i = 0; i < nums.length; i++) {
if (counts[0]) {
nums[i] = 0;
counts[0]--;
} else if (counts[1]) {
nums[i] = 1;
counts[1]--;
} else {
nums[i] = 2;
counts[2]--;
}
}
}感覺稍微有點暴力解,用了兩次迴圈,但多用的空間應該還算符合 in-place,只有 O(1) 而已。
撰寫測試
先用單元測試跑一遍看看是否能符合期待:
describe('Sort Colors', () => {
test.each([
[
[2, 0, 2, 1, 1, 0],
[0, 0, 1, 1, 2, 2]
],
[
[2, 0, 1],
[0, 1, 2]
],
[[1], [1]],
[
[2, 2, 2, 2, 2],
[2, 2, 2, 2, 2]
],
[
Array(100).fill(2).concat(Array(100).fill(1)).concat(Array(100).fill(0)),
Array(100).fill(0).concat(Array(100).fill(1)).concat(Array(100).fill(2))
]
])('should sort %s to %s', (input, expected) => {
sortColors(input);
expect(input).toEqual(expected);
});
});複雜度分析
- 時間複雜度:跑兩次迴圈,如果輸入有 N 個值,則為 2N,因此為
O(n) - 空間複雜度:只額外使用了一個長度為 3 的陣列,所以是
O(1)
進階挑戰或其他解法探索
後來查了下才知道原來這個題目還被叫做荷蘭國旗問題 (Dutch National Flag Problem),因為荷蘭國旗顏色剛好是紅白藍,且此問題最初是由荷蘭知名科學家 Edsger Dijkstra 所提出。
如果是要做到可以在一個迴圈內完成的話,要用三個指標 (three pointers) 來解,解法的思路像以下這樣:
- 使用三個指標:
left:指向應該放置0的位置,初始化為0right:指向應該放置2的位置,初始化為陣列最後一位current:目前檢查的元素,初始化為0
- 跑一個 while 迴圈,直到 current 超過 right 的位置,檢查
nums[current]的值:- 為
0的話,將current與left交換,left++,current++ - 為
2的話,將current與right交換,right--,但不移動current,因為交換後的元素還需檢查 - 為
1的話,current++
- 為
覺得光看文字有點難理解,還是用個範例 [2, 0, 2, 1, 1, 0] 搭配實際畫圖比較好懂:
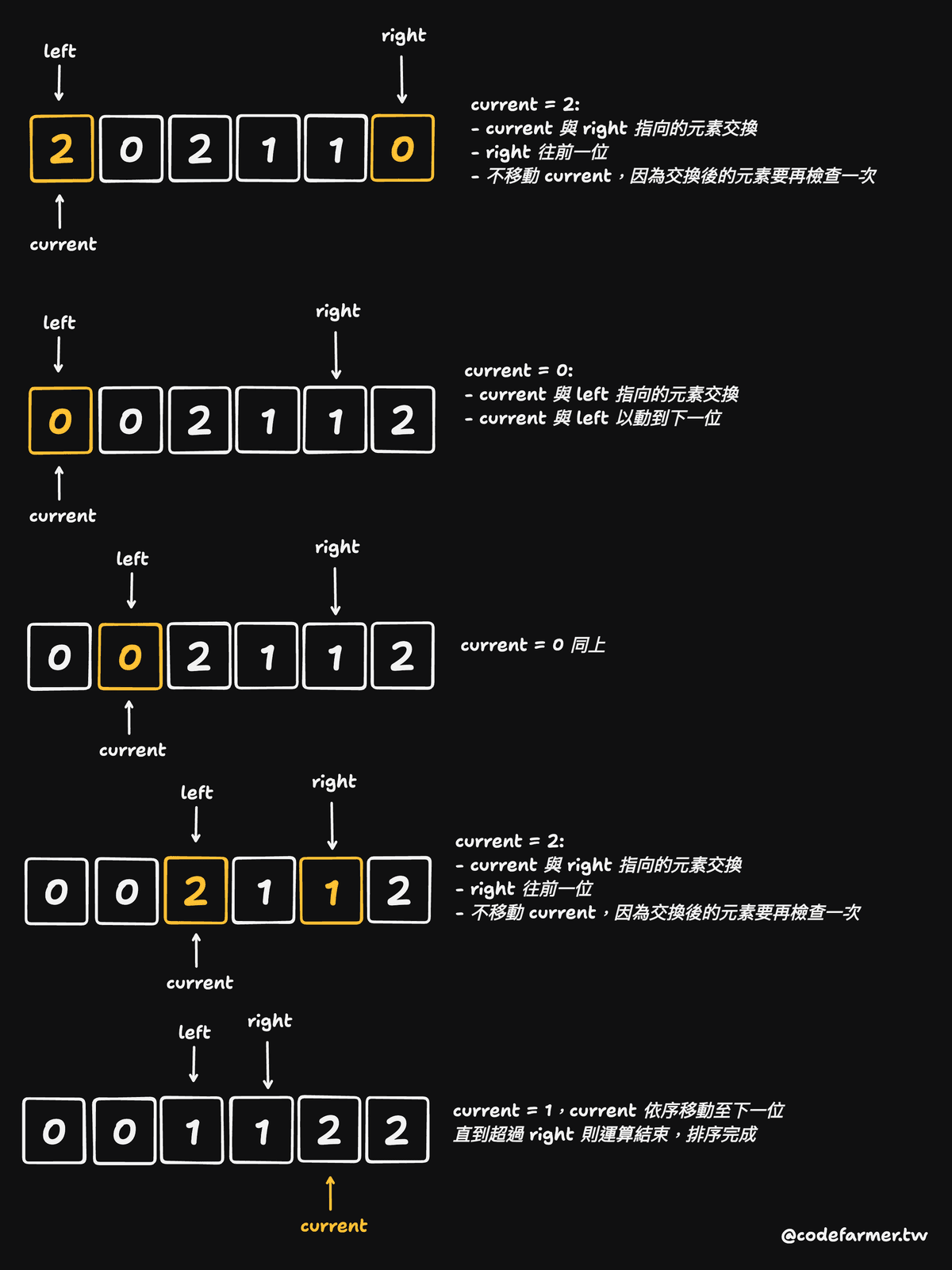
如果依照這個演算法的邏輯,實作起來其實不麻煩:
export function sortColorsThreePointers(nums: number[]): void {
let left = 0;
let right = nums.length - 1;
let current = 0;
while (current <= right) {
if (nums[current] === 0) {
// 交換 left 與 current 指向的元素
[nums[left], nums[current]] = [nums[current], nums[left]];
left++;
current++;
} else if (nums[current] === 2) {
// 交換 right 與 current 指向的元素
[nums[current], nums[right]] = [nums[right], nums[current]];
right--;
} else {
current++;
}
}
}程式碼
詳細程式碼可以參考此 GitHub 連結。
