[M] 3066. Minimum Operations to Exceed Threshold Value II
題目
- LeetCode 連結
- 主題:Heap (Priority Queue)
- 難度:Medium
- Daily:2025-02-13
題目描述
給定一個 0 索引 的整數數組 nums,以及一個整數 k。
每次操作,你可以執行以下步驟:
- 取出
nums中最小的兩個整數x和y。 - 從
nums中移除x和y。 - 將
min(x, y) * 2 + max(x, y)添加回nums。
請注意,當 nums 至少包含兩個元素時,才能執行上述操作。請返回使得 nums 中所有元素都大於等於 k 所需的最少操作次數。
範例 1
輸入:nums = [2,11,10,1,3], k = 10
輸出:2
解釋:
- 第一次操作,移除 `1` 和 `2`,然後加入 `1 * 2 + 2 = 4`,nums 變為 `[4, 11, 10, 3]`。
- 第二次操作,移除 `3` 和 `4`,然後加入 `3 * 2 + 4 = 10`,nums 變為 `[10, 11, 10]`。
- 此時所有數字都大於等於 `10`,可以停止操作。
最少需要 2 次操作使所有數字都大於等於 `10`。範例 2
輸入:nums = [1,1,2,4,9], k = 20
輸出:4
解釋:
- 第一次操作後,nums 變為 `[2, 4, 9, 3]`。
- 第二次操作後,nums 變為 `[7, 4, 9]`。
- 第三次操作後,nums 變為 `[15, 9]`。
- 第四次操作後,nums 變為 `[33]`。
- 此時所有數字都大於等於 `20`,可以停止操作。
最少需要 4 次操作使所有數字都大於等於 `20`。限制條件
2 <= nums.length <= 2 * 10^51 <= nums[i] <= 10^91 <= k <= 10^9- 輸入保證一定存在解,即總能透過某種操作順序,使所有元素大於等於
k。
問題釐清
- 雖然題目限制一定存在符合 k 值條件的解,但為了處理邊界條件,若像是
nums長度小於 2 或找不到解則回傳-1是否可行?
提出思路
這題如果不使用 min heap 來實作的話,直覺應該會是用各種陣列方法來做暴力解,也就是在 while 迴圈中不斷地插入、刪除、檢查當前最小值是否大於等於 k。
而如果能將一開始的 nums 轉成 min heap 的結構,主程式的邏輯就簡潔許多了,效能也好。
實作
稍微學了一下基礎 priority queue 與 heap 的概念後,才發現原來像是 Python 的 heapq、C++ 的 priority_queue、Java、Go 這些語言都有內建 heap 的資料結構,而如果使用 JavaScript/TypeScript 的話,很抱歉,這需要自己實作,甚至有個專門的套件 (@datastructures-js/heap、@datastructures-js/priority-queue) 能直接調用。
2025-03-15 補充:後來經過古古的友情提醒與研究,發現如果是使用 LeetCode 並搭配 JavaScript/TypeScript 進行 PQ 相關的解題時,預設平台是會自動載入上述兩個套件輔助更方便善用像是 min heap 或 max heap 的資料結構 (ref)。而 Python 有另一個限制是原生並沒有提供 max heap,查了下資訊看起來會需要調整成負數形式來用 min heap 實作。
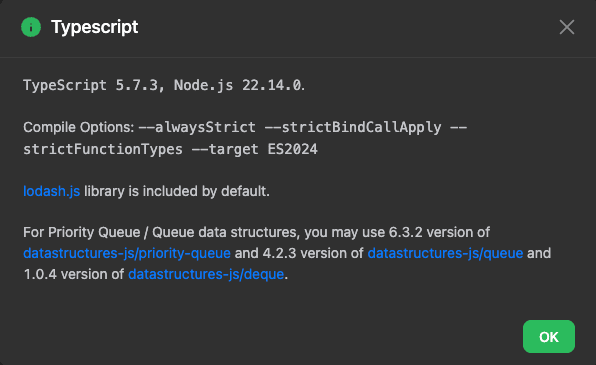
有鑒於上面的補充,直接來嘗試看看使用套件的版本 (LeetCode 上套件版本在 TypeScript 型別編譯上另有差異,需拿掉泛型):
import { MinPriorityQueue } from '@datastructures-js/priority-queue';
function minOperations(nums: number[], k: number): number {
// handle edge case
if (nums.length < 2) {
return -1;
}
// arrange nums with min heap
const pq = new MinPriorityQueue<number>();
nums.forEach(num => pq.enqueue(num));
let count = 0;
// run while loop until array length smaller than h
// check whether all new nums larger or equal to k
while (pq.size() >= 2 && pq.front()! < k) {
const x = pq.dequeue()!;
const y = pq.dequeue()!;
const newNum = Math.min(x, y) * 2 + Math.max(x, y);
pq.enqueue(newNum);
count++;
}
// return minimum operation count
return count;
}純手工實作
雖然實際在 LeetCode 上解題可以直接用套件,還是保留下原本的筆記,如果要純手工實作一個簡單版的 MinHeap class 的話會長這樣:
// @/types/Heap.ts
export class MinHeap<T> {
private heap: T[] = [];
private getParentIndex(i: number): number {
return Math.floor((i - 1) / 2);
}
private getLeftChildIndex(i: number): number {
return 2 * i + 1;
}
private getRightChildIndex(i: number): number {
return 2 * i + 2;
}
private swap(i: number, j: number): void {
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
private heapifyUp(): void {
let index = this.heap.length - 1;
while (index > 0) {
const parentIndex = this.getParentIndex(index);
if (this.heap[index] >= this.heap[parentIndex]) break;
this.swap(index, parentIndex);
index = parentIndex;
}
}
private heapifyDown(): void {
let index = 0;
while (this.getLeftChildIndex(index) < this.heap.length) {
let smallerChildIndex = this.getLeftChildIndex(index);
const rightChildIndex = this.getRightChildIndex(index);
if (
rightChildIndex < this.heap.length &&
this.heap[rightChildIndex] < this.heap[smallerChildIndex]
) {
smallerChildIndex = rightChildIndex;
}
if (this.heap[index] <= this.heap[smallerChildIndex]) break;
this.swap(index, smallerChildIndex);
index = smallerChildIndex;
}
}
push(value: T): void {
this.heap.push(value);
this.heapifyUp();
}
pop(): T | undefined {
if (this.heap.length === 0) return undefined;
if (this.heap.length === 1) return this.heap.pop();
const minValue = this.heap[0];
this.heap[0] = this.heap.pop()!;
this.heapifyDown();
return minValue;
}
peek(): T | undefined {
return this.heap[0];
}
size(): number {
return this.heap.length;
}
isEmpty(): boolean {
return this.heap.length === 0;
}
}有個這個結構後,就能來實作這一題:
import { MinHeap } from '@/types/Heap';
function minOperations(nums: number[], k: number): number {
// handle edge case
if (nums.length < 2) {
return -1;
}
// declare new nums array
const heap = new MinHeap<number>();
for (let num of nums) {
heap.push(num);
}
let count = 0;
// run while loop until array length smaller than h
// check whether all new nums larger or equal to k
while (heap.size() >= 2 && heap.peek()! < k) {
const x = heap.pop()!;
const y = heap.pop()!;
const newNum = Math.min(x, y) * 2 + Math.max(x, y);
heap.push(newNum);
count++;
}
// return minimum operation count
return heap.peek()! < k ? -1 : count;
}複雜度分析
若 N 代表 nums 長度:
- 時間複雜度:
O(NlogN)- 建立 min heap 結構:每次插入元素是
O(logN),執行 N 次所以是O(NlogN) - while 迴圈:
- 取最小值 (peek) 時是
O(1) - 每次 pop 最小值是
O(logN) - 每次 push 新計算的值是
O(logN) - 迴圈執行次數接近 N 次,因此總計為
O(NlogN)
- 取最小值 (peek) 時是
- 建立 min heap 結構:每次插入元素是
- 空間複雜度:另外用了一個 heap 來處理為
O(N)
程式碼
詳細程式碼可以參考此 GitHub 連結。
