[E] 232. 用堆疊實作隊列 (Implement Queue using Stacks)
題目
- LeetCode 連結
- 主題:Stack
- 難度:Easy
題目描述
設計一個僅使用兩個堆疊(stacks)的 先進先出 (FIFO) 隊列 (queue) 結構,並實現正常隊列的所有功能,包括以下操作:
void push(int x)將元素x推入隊列的尾部。int pop()移除並返回隊列的頭部元素。int peek()返回隊列頭部的元素。boolean empty()如果隊列為空,則返回true;否則返回false。
注意:
- 你只能使用堆疊的標準操作,包括:push 到頂部、從頂部 peek/pop、檢查大小和判斷是否為空。
- 如果你的程式語言不支援內建的堆疊,你可以使用列表(list)或雙端隊列(deque)來模擬堆疊,但只能使用堆疊的標準操作。
範例
輸入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
輸出:
[null, null, null, 1, 1, false]
解釋:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // 隊列為: [1]
myQueue.push(2); // 隊列為: [1, 2](左邊是隊列頭部)
myQueue.peek(); // 返回 1
myQueue.pop(); // 返回 1,隊列變為 [2]
myQueue.empty(); // 返回 false
限制條件
1 <= x <= 9- 對
push,pop,peek, 和empty的調用次數最多為100次。 - 所有對
pop和peek的調用都是有效的(即在調用之前隊列不為空)。
進階挑戰
你能否實現所有操作的攤銷 (amortized) 時間複雜度為 O(1)?換句話說,執行 n 個操作的總時間為 O(n),即使某些操作可能需要更長的時間。
問題釐清
- 因為是要模擬 queue 的行為,所以這裡的 push 指的是 enqueue、pop 指的是 dequeue,為了避免溝通混肴,以下是否可以改名成
enqueue與dequeue - 執行 enqueue 後是否不需回傳任何值?
- 執行 peek 後是只要回傳當前 queue 的首位值而已,不需移除對吧?
- 當 queue 為空時,執行 dequeue 或 peek 時是否需回傳 null 視為不存在?
- 「只能使用堆疊的標準操作」,以 JavaScript 來說就是只能用 array 的 push、pop 兩個方法,而不能用 shift、unshift?那 concat 可以用嗎?
提出測試案例
- 測試範例的基本案例能回傳正確值
- 當 queue 為空時,執行 dequeue 與 peek 也不會噴錯
提出思路
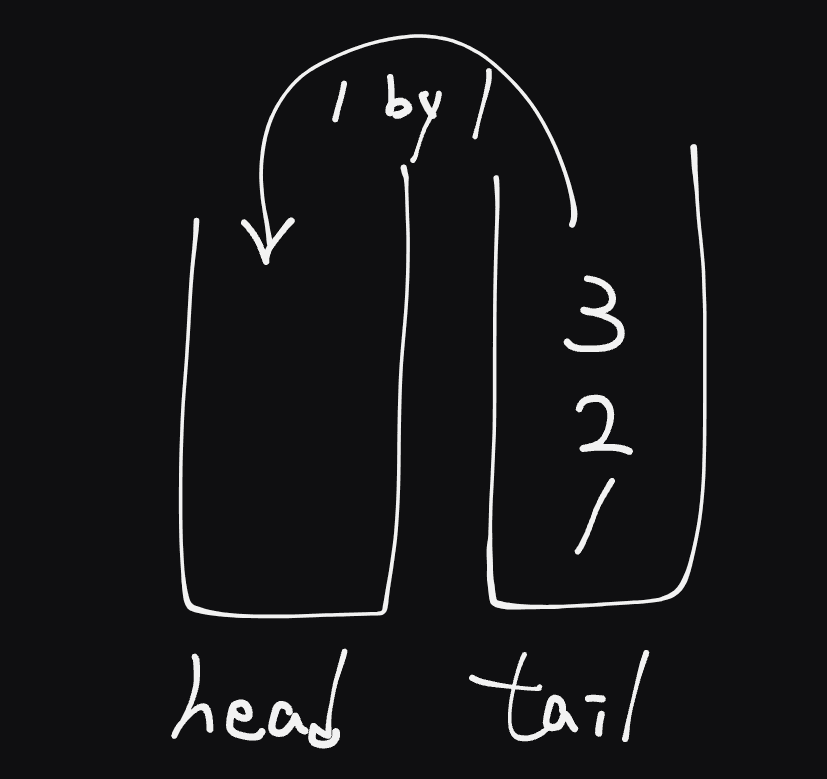
因為是需要用兩個 stack 來模擬 queue 的結構,所以在執行每個要參考 queue 頭部的操作 dequeue 與 peek 時會需要多一些判斷來調整資料順序:
- 宣告 head、tail 兩個 stack array:
- head 模擬 queue 的頭部
- tail 負責放入新推入的值
- enqueue:將值直接推入 tail 中
- dequeue:檢查 head 中是否有值
- 是:pop 出 head 堆疊中的上方元素
- 否:檢查 tail 是否有值
- 是:一個一個 pop 出來並 push 到 head 中,再 pop 出 head 堆疊中的上方元素
- 否:回傳 null
- peek:同 dequeue 邏輯,但只讀取 head 的最末端元素值不執行 pop
- empty:檢查兩個 stack 是否皆為空
以註解表示,這裡因為 dequeue 與 peek 有相同邏輯,另外抽成一個 static method 來避免重複:
class MyQueue {
// declare head and tail stack arrays
constructor() {}
enqueue(x: number): void {
// push x into tail directly
}
// implement a private method to manipulate two stack for `dequeue` adn `peek`
private swapStack() {
// check and swap values from tail to head
}
dequeue(): number {
// check empty status, if true, return null
// do swapCheck
// return and pop value from head
}
peek(): number {
// check empty status, if true, return null
// do swapCheck
// return value from head
}
empty(): boolean {
// check if two stack are all empty
}
}實作
根據上述的註解來實作,實作完後將原本 enqueue 與 dequeue 改回 push 與 pop 符合題目要求:
export class MyQueue {
// declare head and tail stack arrays
private head: number[];
private tail: number[];
constructor() {
this.head = [];
this.tail = [];
}
push(x: number): void {
// push x into tail directly
this.tail.push(x);
}
// implement a private method to manipulate two stack for `dequeue` adn `peek`
private swapStack(): void {
// check and swap values from tail to head
const { head, tail } = this;
if (head.length === 0) {
while (tail.length !== 0) {
head.push(tail.pop() as number);
}
}
}
pop(): number | null {
// check empty status, if true, return null
if (this.empty()) {
return null;
}
// do swapCheck
this.swapStack();
// return and pop value from head
const headValue = this.head.pop() as number;
return headValue;
}
peek(): number | null {
// check empty status, if true, return null
if (this.empty()) {
return null;
}
// do swapCheck
this.swapStack();
// return value from head
return this.head[this.head.length - 1];
}
empty(): boolean {
// check if two stack are all empty
return this.head.length === 0 && this.tail.length === 0;
}
}關於進階挑戰
在題目的進階挑戰中提到希望可能在某些操作像是 pop 與 peek 時,只有在 head 為空的狀況下才會做交換 stack 資料,而讓時間複雜度到 O(N),但其他狀況與 push 與 empty 都是 O(1),所以在操作夠平均下來理論上能接近 O(1)。
那怎樣會讓進階挑戰不成立呢,可能就像是連 push 都去做交換 stack 的資料,每次都組合成 queue 的模樣,就會讓攤銷下來的時間接近 O(N)。
程式碼
詳細程式碼可以參考此 GitHub 連結。
